Существующие треугольники

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

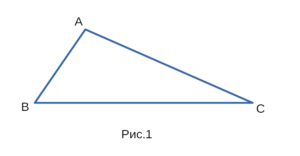
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

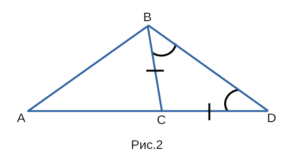
1. Проведем отрезок CD равный отрезку CB.
2. △BCD — равнобедренный, значит ∠CBD = ∠CDB.
3. Рассмотрим △ABD: ∠ABD > ∠CBD, следовательно ∠ABD > ∠CDB, то AB < AD.
4. Но AD = AC + CD = AC + CB, поэтому AB < AC + CB, ч.т.д.

Следствия из теоремы

1. Для любых точек А, В, С, не лежащих на
   одной прямой справедливы неравенства:
   AB < AC + BC
   AC < AB + BC
   BC < AC + AB
   
2. Каждая сторона треугольника меньше суммы двух других сторон.
3. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним углов.
4. Теорема о неравенстве треугольника для разности сторон.

Признаки существования треугольника

• Если каждая сторона треугольника меньше суммы двух других сторон, значит треугольник существует.
• Если большая сторона треугольника меньше суммы двух других сторон,
  значит треугольник существует.
• Если сумма углов треугольника равна 180°, значит треугольник существует.