Признаки параллелограмма — это признаки,
с помощью которых можно доказать,
что четырехугольник — параллелограмм.
Чтобы доказать, что четырехугольник — параллелограмм, нужно знать признаки
параллелограмма. Четырехугольник является параллелограммом, если один
из признаков параллелограмма для этого четырехугольника истинен.
Например, если у четырехугольника две стороны равны и
параллельны, значит этот четырехугольник параллелограмм.
Всего существует три признака параллелограмма: по двум одинаковым
параллельным сторонам, по пересечению диагоналей и делению
диагоналей пополам в точке пересечения, по попарно равным
противоположным сторонам. В этой статье мы рассмотрим
все три признака параллелограмма.
I признак параллелограмма
По пересечению диагоналей и делению
диагоналей в точке пересечения пополам.
Четырехугольник является параллелограммом, если у четырехугольника
диагонали пересекаются, и в точке пересечения делятся пополам.
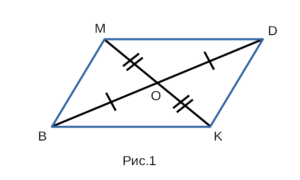
Если на рисунке 1 — BO = OD, MO = OK, то BMDK — параллелограмм.
II признак параллелограмма
По двум одинаковым параллельным сторонам.
Четырехугольник является параллелограммом, если у четырехугольника
две стороны равны и параллельны.
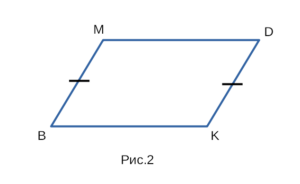
Если на рисунке 2 — BM = DK, BM || DK, то BMDK — параллелограмм.
III признак параллелограмма
По попарно равным противоположным сторонам.
Четырехугольник является параллелограммом, если у
четырехугольника противоположные стороны попарно равны.
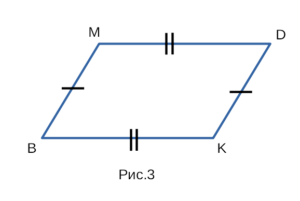
Если на рисунке 3 — BM = DK, MD = BK, то BMDK — параллелограмм.
В этой статье мы рассмотрели все три признака параллелограмма и теперь можем доказать, что некий четырехугольник параллелограмм. Осталось вспомнить что вы знаете про свойства параллелограмма и можно будет сказать вы знаете о нём всё.
В следующей статье про площадь параллелограмма вы узнакете как её расчитать.









