Свойства параллелограмма

Для того, чтобы уметь решать задачи связанные с параллелограммом, нужно
знать свойства параллелограмма. В этой статье будет рассказано об  свойствах
параллелограмма, которые могут вам пригодится при решении задач.

Перечислим свойства параллелограмма, используя рисунок 1. На рисунке 1
изображен параллелограмм APCQ с центром симметрии в точке O.

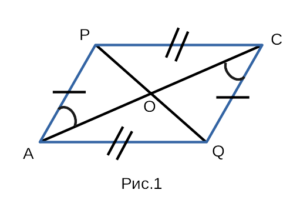
1. У параллелограмма противоположные стороны равны.
   AP = CQ, PC = AQ.
2. У параллелограмма противоположные стороны параллельны.
   AP || CQ, PC || AQ
3. Противоположные углы параллелограмма равны.
   ∠PAQ = ∠PCQ, ∠APC = ∠AQC.
4. Как и в любом другом выпуклом четырехугольнике сумма углов в
   параллелограмме 360°. ∠A + ∠P + ∠C + ∠Q = 360°.
5. Сумма двух углов прилегающих к любой из сторон параллелограмма
   равна 180°. ∠A + ∠P = 180°, ∠C + ∠Q = 180°, ∠P + ∠C = 180°, ∠A + ∠Q = 180°.
6. Диагональ делит параллелограмм на два одинаковых треугольника.
   У параллелограмма только две диагонали. △APC = △AQC, △PAQ = △PCQ.
7. Две диагонали параллелограмма делят его на четыре одинаковых треугольника.
   △APC, △AQC, △PAQ, △PCQ.
8. В параллелограмме две диагонали пересекаются в точке пересечения, и также
   делят друг друга пополам. O — точка пересечения, AO = OC, PO = OQ.
9. Центр симметрии параллелограмма — это точка где пересекаются диагонали
   параллелограмма. O — точка симметрии.
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
    PQ² + AC² = 2AP² + 2PC²
11. Биссектрисы противоположных углов параллелограмма всегда параллельны.
12. Биссектрисы соседних углов параллелограмма всегда пересекаются
    под прямым углом 90°.

Теперь, когда вы знаете все свойства параллелограмма, вы можете с легкостью
решить любую задачу с параллелограммами. Также можно рассчитать площадь параллелограмма.