Четырехугольник — это многоугольник, у которого четыре угла
и четыре стороны.
Противоположными сторонами называются две не смежные стороны
многоугольника, а углы, которые не являются соседними называются
противоположными углами.
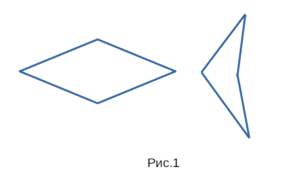
Существуют два вида четырехугольников — выпуклые и не выпуклые. На
рисунке 1 изображены слева изображен один выпуклый и справа
один не выпуклый четырехугольники.
У четырехугольника также есть две диагонали. Каждая из диагоналей выпуклого
четырехугольника делит его на два треугольника. В сумме две диагонали
четырехугольника делят его на четыре треугольника. Также, и в не выпуклом
треугольнике одна из диагоналей делит его на два треугольника.
Используя формулу: (n-2)*180, где n — количество сторон, можно рассчитать сумму
углов выпуклого четырехугольника. Например, сумма углов выпуклого
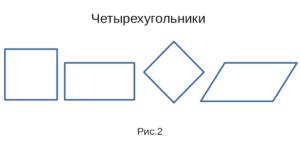
четырехугольника равна 360 градусам. На рисунке 2 изображены четыре
четырехугольника: квадрат, прямоугольник, ромб и параллелограмм.
Геометрические фигуры, такие как, например квадрат, ромб, прямоугольник,
параллелограмм являются четырехугольниками. Фигуры, которые я привел в
пример обладают рядом уникальных свойств, характерных только для них.
Например зная, что у некоего четырехугольника четыре стороны или угла равны,
можно сказать, что это квадрат.
Чтобы узнать какую геометрическую фигуру представляет из себя четырехугольник,
нужно как минимум знать его стороны или углы. Например, если в задаче которую вы
решаете, говорится о том, что в некоем четырехугольнике — все углы равны, то знайте,
что этот четырехугольник — квадрат.
Больше узнать о выпуклых четырехугольниках можно узнать в статье — Выпуклый многоугольник.









