Четвертый признак равенства треугольников

Четвертый признак равенства треугольников — это признак,
c помощью которого можно доказать, что треугольники равны.

С помощью четвертого признака равенства можно решить
любую из задач, где требуется доказать, что треугольники равны.

Формулировка:

Если две стороны и угол, лежащий против большей из сторон
одного треугольника соответственно равны двум сторонам и углу,
лежащему против большей из сторон другого треугольника,
то такие треугольники равны.

Докажем, что △ABC и △FHE равны между собой. Для этого
совместим их так, как показано на рисунке 1.

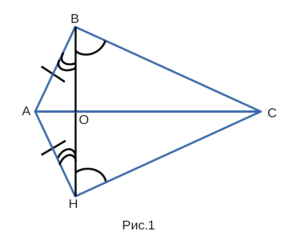
Доказательство:

1. Рассмотрим △ABC и △FHE, которые наложились друг на друга,
   AВ = AH,  ∠ABO = ∠AHO, ∠BOC = ∠HOC. Докажем, что △ABC = △FHE.
2. △ABH — равнобедренный (AB = AH), значит ∠ABO = ∠AHO.
3. ∠BOC = ∠HOC, так как остатки равных углов.
4. △BHC — равнобедренный(∠BOC = ∠HOC), а так как углы при боковых
   сторонах HC и BC равны, значит HC = BC.
5. Итак, △ABC = △FHE по двум сторонам и углу, лежащему
   против большей из сторон.

Также не забудьте прочитать третий признак равенства треугольников.