Трапеция

Трапеция — это четырехугольник, у которого только две стороны параллельны,
а две другие стороны нет.

Элементы трапеции

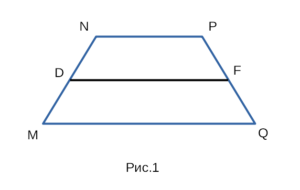
На рисунке 1 изображена трапеция MNPQ, с боковыми сторонами MN и PQ, с основаниями NP и MQ, а также со средней линией DF.

В трапеции две параллельные стороны называются основаниями. 0дна из параллельных сторон называется верхним основанием, а другая параллельная сторона называется нижним основанием. Но как определить, какая из параллельных сторон нижнее основание, а какая верхнее основание? Существует несколько способов это определить. Во-первых, как вы уже наверно догадались, нижнее основание расположено внизу трапеции, а верхнее основание расположено вверху трапеции. Во-вторых, верхнее основание меньше чем нижнее основание, и наоборот нижнее основание больше верхнего основания. C помощью этих двух способов вы можете
легко определить какое основание нижнее а какое верхнее. NP || MQ, NP — верхнее основание, MQ — нижнее основание.

Кроме оснований в трапеции, есть еще две не параллельные стороны. В трапеции эти две не параллельные стороны называются боковыми сторонами. Боковые стороны расположены сбоку от верхнего и нижнего оснований. MN и PQ — боковые стороны.

Отрезок, соединяющий середины боковых сторон называется средней линией трапеции. С средней линией трапеции связано несколько важных формул. Например, достаточно знать длину средней трапеции и одну из сторон основания, чтобы найти другое основание. Средняя линия делит две боковые стороны трапеции на две равных части. DF — средняя линия трапеции, MD = DN, QF = FP.

Центром симметрии трапеции называется середина средней линии трапеции. Центр симметрии
является центром вписанной, и центром описанной окружностей.

Виды трапеции

Также существует несколько видов трапеции. Это равнобедренная и прямоугольная трапеции.

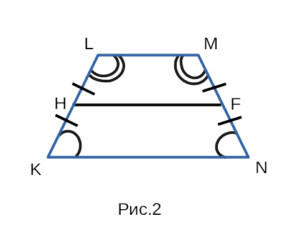
На рисунке 2 изображена равнобедренная трапеция KLMN, с боковыми сторонами KL и MN, с основаниями LM и KN, а также со средней линией HF.

В равнобедренной трапеции боковые стороны равны, углы при основаниях равны. KL = MN, ∠LKN = ∠MNK, ∠KLM = ∠NML.
Чтобы найти среднюю линию в равнобедренной трапеции достаточно знать только одну из боковых сторон.

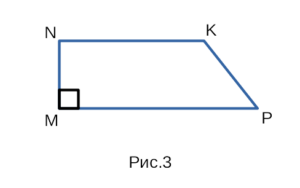
На рисунке 3 изображена прямоугольная трапеция MNKP, с боковыми сторонами MN и KP, с основаниями NK и MP, а также с прямым углом ∠NMP .

В прямоугольной трапеции у одной из боковых сторон есть прямой угол, или же по другом сказать — только одна боковая сторона перпендикулярна одному из оснований.
∠NMP — прямой угол.

Свойства трапеции

1. В трапеции может быть вписанная окружность, лишь в том случае, если сумма длин оснований трапеции равна сумме длин боковых сторон.
2. В трапеции средняя линия делит пополам её основания, и также делит пополам диагонали.
3. В трапеции нижнее и верхнее основания параллельны друг другу.
4. Средняя линия параллельна верхнему и нижнему основанию.
5. В трапеции могут находится только две диагонали. Точка, где пересекаются диагонали лежит на одной прямой.

Признаки трапеции

1. Трапецией является четырехугольник, у которого только две стороны параллельны,
   а две другие стороны нет.
2. Равнобедренной трапецией является трапеция, у которого две боковые стороны равны.
3. Равнобедренной трапецией является трапеция, у которой при любом из оснований углы равны.
4. Прямоугольной трапецией является трапеция, у которой один из углов при основании прямой.