Теорема Пифагора является одной из важнейших теорем в геометрии.
Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
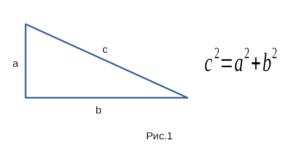
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.
Доказательство теоремы Пифагора
Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).
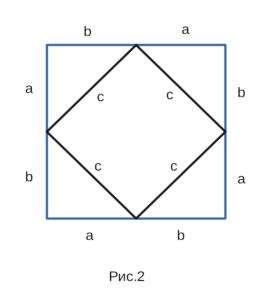
Достроим наш прямоугольный треугольник до квадрата, изображенного
на рисунке 2. Квадрат, который мы построили состоит из четырех равных
прямоугольных треугольников. Площадь каждого прямоугольного треугольника
равна \( (1/2)ab \), а площадь всего квадрата \( (a+b)^2 \), поэтому:
\( S = 4 * (1/2)ab + c^2 = 2ab + c^2. \).Тогда, \( (a+b)^2 = 2ab + c^2 \), откуда
следует, что \( c^2=a^2+b^2 \). ч.т.д.
Теорема доказана.
Следствия из теоремы Пифагора
У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них:
- В прямоугольном треугольнике гипотенуза больше любого из катетов.
- Площадь прямоугольного треугольника равна половине произведения одного катета на другой катет.
- Треугольник прямоугольный, если к любым двум сторонам треугольника можно применить теорему Пифагора и найти третью сторону.
- \( c^2=a^2+b^2 \)
- \( a^2=c^2-b^2 \)
- \( b^2=c^2-a^2 \)