Сумма Углов Прямоугольного Треугольника — Доказательство, Теорема

Теорема о сумме углов прямоугольного треугольника

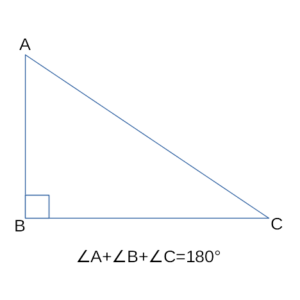
Сумма углов прямоугольного треугольника равна 180°

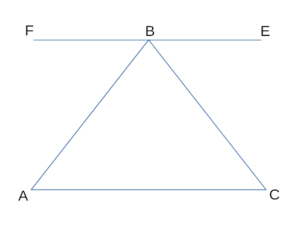
Докажем, что в любом треугольнике сумма углов 180°:

1. АBC  — треугольник
2. Доп. построение: через вершину B проведем прямую FE параллельно основанию AC
3. ∠CBE=∠C(внутренние накрест лежащие при параллельных FE$\parallel$AC, и секущей BC) и$\angle FBA=\angle$A(внутренние накрест лежащие при  $FE\parallel AC,$ и секущей AB)
4. ∠FBE=∠FBA+∠B+∠CBE(так как развернутый) ⇒ 180°=$\angle$A+$\angle$B+$\angle$C ч.т.д.

Сумма острых углов прямоугольного треугольника равна 90°

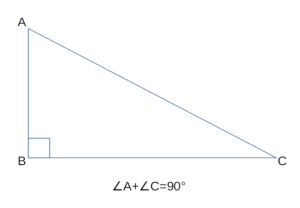
Докажем, что в прямоугольном треугольнике сумма острых углов 90°:

1. △ABC- прямоугольный
2. ∠B — прямой(так как △ABC- прямоугольный)
3. ∠A+∠B+∠C=180°(сумма углов треугольника) ⇒ ∠А+∠C=180°-∠B ⇒ ∠A+∠C=90° ч.т.д

Следствия из доказанных теорем:

1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.