Теорема о соотношениях между углами и сторонами
треугольника звучит так:
В треугольнике напротив большего угла лежит
большая сторона, и обратно, напротив большей
стороны лежит больший угол.
Доказательство теоремы
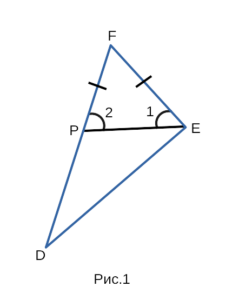
Эту теорему мы докажем, используя рисунок 1, где изображен
треугольник DFE.
1. Предположим, что в треугольнике DFE сторона FE < DF.
Докажем, что ∠E >∠D.
Отложим на стороне DF отрезок FP = FE. В результате ∠1 = ∠2,
а сторона PF = FE, следовательно треугольник PFE — равнобедренный.
∠1 является частью ∠E, значит ∠1 < ∠С. ∠2 — внешний угол
треугольника PDE, поэтому∠2 > ∠D. Так, как ∠1 и ∠2 равны, а ∠1
является частью ∠E, ∠2 > ∠D, значит ∠E > ∠D.
2. Допустим, что в треугольнике DFE ∠E > ∠D. Докажем,
что сторона FD > FE.
Предположим, что это не так. Тогда сторона FD = FE, или сторона FD < FE.
В первом случае треугольник FDE — равнобедренный, значит∠E = ∠D.
Во втором же случае ∠D > ∠E — напротив большей стороны лежит больший угол.
Утверждение в первом и втором случае противоречит условию: ∠E > ∠D. Из этого
следует то, что наше предположение неверно, и, следовательно DF > FE, ∠E >∠D, ч.т.д.
Теорема доказана.
Следствия из доказанной теоремы
Из теоремы, которую мы сейчас доказали следует вот что:
- Гипотенуза в прямоугольном треугольнике больше катета,
так как катеты лежат напротив острых углов, а гипотенуза
лежит напротив прямого угла. - Если две стороны или два угла треугольника равны, то
треугольник равнобедренный, действительно, если в
треугольнике два угла равны, значит и стороны
напротив этих углов равны. - В равнобедренном треугольнике при равных сторонах два
угла равны, а третий больший угол лежит
напротив большей стороны.









