Перпендикулярные прямые — это две пересекающиеся прямые,
образующие четыре прямых угла.
По другому можно сказать так: перпендикулярные
прямые — это две прямые, которые пересекаются под прямым углом.
Эти два утверждения истинны.
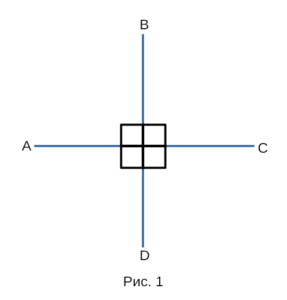
Перпендикулярность прямых обозначается символом ⊥. Например,
перпендикулярность прямых, изображенных на рисунке 1 обозначается
так: AC⊥BD. А читается так: прямая AC перпендикулярна к прямой BD.
Для того, чтобы начертить перпендикулярные прямые используют
чертежный угольник и линейку.
Две прямые, перпендикулярные к третьей не пересекаются,
но параллельны между собой.
- Перпендикуляр — это прямая опущенная под прямым углом
к другой прямой. - Перпендикуляр к данной прямой — это отрезок прямой,
перпендикулярный данной прямой, имеющий одним из
своих концов их точку пересечения. - Основание перпендикуляра — это конец отрезка прямой,
которая перпендикулярна данной прямой.
Условие перпендикулярности двух прямых — две прямые
пересекаются под прямым углом.
Из точки, не лежащей на прямой, можно провести
перпендикуляр к этой прямой, и притом только один.Прямая перпендикулярна плоскости, если она
перпендикулярна любой прямой, лежащей
в этой плоскости.









