Определение
Параллельными прямыми называются две прямые,
которые не пересекаются.
Параллельность прямых обозначают знаком: ∥. Например
параллельность прямых a и b обозначается так: a ∥ b.
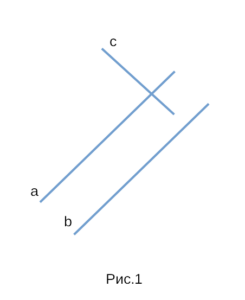
На рисунке 1 изображены три прямые. Прямая а параллельна
прямой b, прямая c не параллельна ни одной из прямых.
Также, как и параллельные прямые, существуют параллельные
отрезки. Два отрезка называются параллельными, если они
лежат на параллельных прямых.
Признаки
Параллельность двух прямых можно доказать по трем признакам.
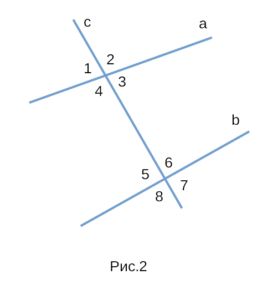
На рисунке 2 изображены 8 углов, при помощи которых можно
доказать все три признака параллельности. Это накрест лежащие
углы: 3 и 5, 4 и 6; односторонние углы: 4 и 5, 3 и 6;
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Прямая называется секущей по отношению к двум другим прямым,
если она пересекает их в двух точках.
- Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые параллельны. - Если при пересечении двух прямых секущей
соответственные углы равны, то прямые параллельны. - Если при пересечении двух прямых секущей
сумма односторонних углов равна 180°, то прямые параллельны.









