Определение медианы
Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.
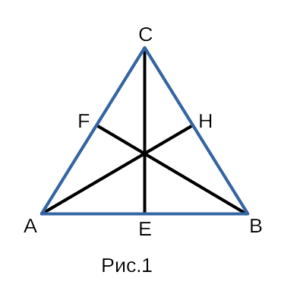
На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.
Свойства медианы
- Медиана делит противолежащую сторону пополам.
- Медиана разбивает равнобедренный треугольник на два треугольника.
- Медианы треугольника пересекаются в одной точке.
- Медиана равнобедренного треугольника, проведенная к основанию,
является биссектрисой и медианой. - Любой треугольник имеет три медианы.
- Три медианы разбивают треугольник на шесть
равных треугольников.
Признаки медианы
- Отрезок имеющий начало в вершине треугольника и конец на середине
противоположной стороне является медианой. - В прямоугольном треугольнике отрезок проведенный из вершины
прямого угла к гипотенузе, является медианой. - Отрезок проведенный из вершины равнобедренного треугольника является
высотой и биссектрисой, и также является медианой. - В треугольнике точкой пересечения отрезки делящиеся
в отношении 2:1, то они являются медианами.









