Признаки, Свойство и Определение Квадрата

Определение

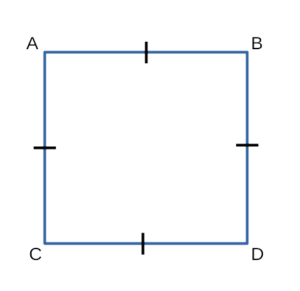
Квадрат — это четырехугольник, имеющий равные стороны и углы.
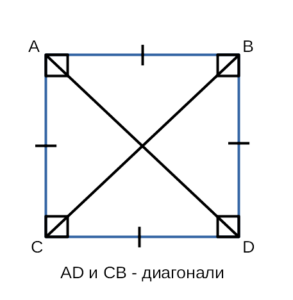
Диагональ квадрата — это отрезок, соединяющий две
его противоположные вершины.

Свойства квадрата

В квадрате:

1. Длины сторон квадрата равны.
2. Все углы квадрата прямые.
3. Противолежащие стороны квадрата параллельны друг другу.
4. Сумма всех углов квадрата равна 360°.
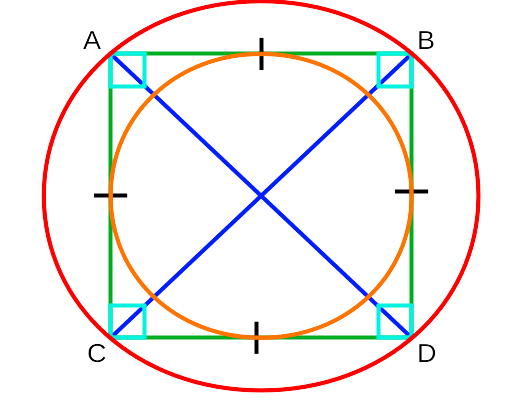
5. Центр описанной и вписанной окружности — точка пересечения диагоналей квадрата.
6. Диагонали квадрата равны, перпендикулярны и разделяются точкой пересечения пополам.

Признаки квадрата

С помощью признаков квадрата можно доказать, что четырехугольник — квадрат.

1. По сторонам и углу 90°:
   Если в четырехугольнике все стороны равны и один из углов 90°, то это квадрат.
2. По диагоналям:
   Если диагонали четырехугольника равны, перпендикулярны и делятся пополам в точке пересечения, то это квадрат.
3. По ромбу:
   Если в ромбе все углы прямые, то это квадрат.
4. По прямоугольнику:
   Если в прямоугольнике все стороны равны, то это квадрат.
5. По параллелограмму:
   Если в параллелограмме все стороны и углы равны, то это квадрат.