Теорема косинусов

Чтобы найти строну или угол треугольника применяют Теорему Косинусов.
Эта теорема обобщает теорему Пифагора. Доказать Теорему
Косинусов достаточно просто через треугольник, который
разделяют высотой на два прямоугольных треугольника.

Мы рассмотрим доказательство, формулировку,
следствия из Теоремы Косинусов.

Наряду с одной из известных теорем геометрии — теоремой Пифагора,
существует теорема косинусов. Теорема косинусов похожа по теорему
Пифагора, но отличается. Теорему косинусов, можно применить к абсолютно
любым треугольникам. А теорема Пифагора применяется исключительно
для прямоугольных треугольников.

Теорема косинусов — это теорема геометрии, обобщающая
теорему Пифагора, применяющаяся при нахождении углов
и сторон в любых треугольниках.

Формулировка теоремы косинусов

Формулировка у теоремы косинусов такая: в треугольнике квадрат любой из сторон
 равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между ними. Запишем эту
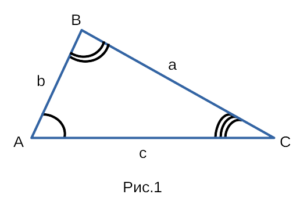
формулировку более кратко, используя рисунок 1, на котором изображен
произвольный треугольник ABC:​  \( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A \)​.
Или,  же еще более кратко: ​ \( a^2 = b^2 + c^2 — 2bc * cos ∠A \)​.

Доказательство теоремы косинусов

Для доказательства теоремы косинусов воспользуемся
рисунком 2, на котором изображен треугольник ABC.

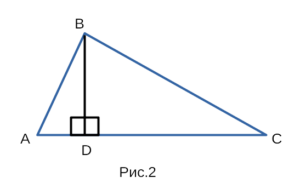
Докажем, что ​\( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A: \)

1. Доп. построение: высота BD.
2. Рассмотрим △BDC:
   ​\( BC^2= BD^2 + DC^2. \)
   
3. Рассмотрим △ABD:
   ​\( AD = AB * cos ∠A, \)​
   ​\( BD = AB * sin ∠A, \)​
   ​\( CD = AC — AD = AC — AB cos ∠A. \)​
4. Из всего этого следует, что: ​
   \( ВС^2 = (AB * sin ∠A)^2 + (AC — AB * cos ∠A)^2 = \)​
   \( AB^2 * sin^2 ∠A + AC^2 — 2AB * AC * cos ∠A + AB^2 * cos^2 ∠A = \)
   \( AB^2 + AC^2 — 2 * (AB*AC) * cos ∠A. \)
   Следовательно, ​\( BC^2 = AB^2 + AC^2 — 2 * (AB * AC) * cos ∠A. \)​ч.т.д.
5. Теорема косинусов доказана.

Следствия из теоремы косинусов

1. Квадрат любой из сторон треугольника равен сумме квадратов двух
   других сторон минус удвоенное произведение этих
   сторон на косинус угла между ними.
2. ​\( a^2 = b^2 + c^2 — 2bc * cos ∠A \)​;
   ​\( b^2 = c^2 + a^2 — 2ca * cos ∠B \)​;
   ​\( c^2 = a^2 + b^2 — 2ab * cos ∠C \)​;
3. Так, как в прямоугольном треугольнике один из углов равен 90 градусам,
   следовательно теорема косинусов преобразуется в теорему Пифагора.
4. С помощью теоремы косинусов, можно определить косинус
   любого из углов треугольника.
5. Если, b² + c² — a² > 0,  ∠A будет острый.
   Если b² + c² — a² = 0, ∠A  будет прямым.
   Если b² + c² — a² < 0,  ∠A будет тупым.

Значение теоремы косинусов

Где применяется теорема косинусов?

Теорема косинусов применяется в тригонометрии, в частности
при нахождение сторон и углов в любых треугольниках. Например, зная
формулировку теоремы косинусов, косинус одно из угла треугольника,
и две стороны можно найти неизвестную сторону треугольника.

Виды теорем косинусов.

В зависимости от свойств треугольника, длины его сторон, градусной меры
его углов — теорема косинусов немного видоизменяется. Например, в
прямоугольных треугольниках теорема косинусов преобразуется в теорему Пифагора.