Определение стороны окружности
Сторона окружности — это длина дуги окружности.
Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.
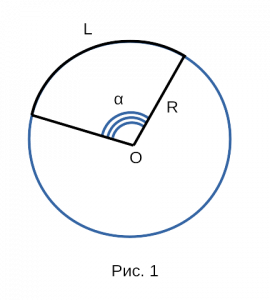
На рисунке 1, изображена окружность,
обладающая следующими величинами:
- O — точка, являющаяся
центром окружности; - R — радиус
окружности; - α — центральный
угол окружности; - L — сторона
окружности;
Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:
Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.
Также, все это можно сделать, зная одну из
известных формул стороны окружности:
\[ L = \frac{ \pi R}{180} \cdot \alpha \]
Формулы стороны окружности
Ⅰ. Через диаметр и центральный угол
Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.
\[ L = \frac{ \frac{D}{2} \cdot \pi}{180} \cdot a \]
Ⅱ. Через площадь и центральный угол
\[ L = \frac{ \sqrt{\frac{S}{\pi}} \cdot \pi}{180} \cdot \alpha \]
Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.
Ⅲ. Через периметр и центральный угол
\[ L = \frac{\frac{P}{2\pi}\cdot \pi}{180} \cdot \alpha \]
Самая краткая запись формулы
стороны окружности.
Пример решения задач по теме сторона окружности
Возьмем для удобства π равное 3.14.
Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?
Решение:
\( L = \frac{\frac{6}{180} \cdot \pi}{180} \cdot 180 = \frac{3 \pi}{180} \cdot 180 = 3\pi = 9.42 \)
Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?
Решение:
\( L = \frac{100}{180} \cdot 60 = 0.55 \cdot 60 = 33 \)









