Признаки равенства прямоугольников

Признаки равенства прямоугольников — это признаки, c
помощью которых можно доказать, что прямоугольники равны.

В этой статье мы рассмотрим и докажем четыре признака
равенства прямоугольников. С помощью этих признаков
можно доказать, равенство двух и более геометрических
фигур — в данном случае прямоугольников.

I признак равенства прямоугольников

По двум неравным сторонам.

Формулировка первого признака равенства
прямоугольников:

Если две неравных стороны одного прямоугольника
соответственно равны двум неравным сторонам другого
прямоугольника, то такие прямоугольники равны.

Докажем, что прямоугольники ABDC и EFPH,
изображенные на рисунке 1 равны между собой.

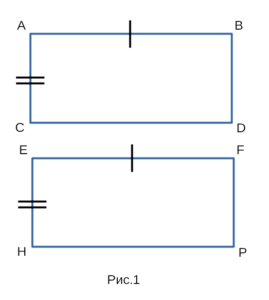
Доказательство первого признака равенства
прямоугольников:

1. Рассмотрим прямоугольники ABDC и EFPH, в которых
   AB = EF, AC = EH. Докажем, что прямоугольники
   ABDC и EFPH равны.
2. AB = EF, значит сторону AB можно наложить на сторону
   EF так, что сторона AB совместится со стороной EF.
3. AC = EH, значит сторону AC можно наложить на сторону
   EH так, что сторона AC совместится со стороной EH.
4. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

II признак равенства прямоугольников

По сумме квадратов двух неравных сторон.

Формулировка второго признака равенства
прямоугольников:

Если сумма квадратов двух неравных сторон одного прямоугольника
соответственно равна сумме квадратов двух неравных сторон
другого прямоугольника, то они равны.

Докажем, что прямоугольники ABDC и EFPH,  изображенные
на рисунке 2 равны между собой.

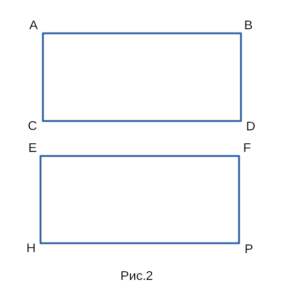
Доказательство второго признака равенства
прямоугольников:

1. Рассмотрим ABDC и EFPH, в которых AB² + ВD² = EF² + FP².
   Докажем, что прямоугольники ABDC и EFPH равны.
2. AB ²+ ВD² = EF² + FP², значит стороны  AB и BD можно наложить
   на стороны EF и FP, так что: сторона AB совместится со стороной EF,
   сторона BD совместится со стороной FP.
3. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

III признак равенства прямоугольников

По диаметру описанной окружности.

Формулировка третьего признака равенства
прямоугольников:

Если диаметр описанной окружности одного прямоугольника
соответственно равен диаметру описанной окружности другого
прямоугольника, то такие прямоугольники равны.

Докажем, что прямоугольники ABDC и EFPH,  изображенные
на рисунке 3 равны между собой.

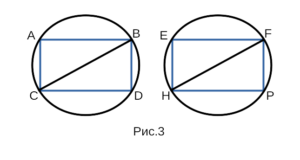
Доказательство третьего признака равенства
прямоугольников:

1. Рассмотрим ABDC и EFPH, в которых CB = HE. Докажем,
   что прямоугольники ABDC и EFPH равны.
2. CB = HE, значит диаметры СВ и HE можно наложить друг
   на друга так, что они совместятся: диаметр СВ совместится
   с диаметром HE.
3. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

IV признак равенства прямоугольников

По равным и параллельным противоположным сторонам.

Формулировка четвертого признака равенства
прямоугольников:

Если противоположные стороны одного прямоугольника соответственно
параллельны и равны противоположным сторонам другого прямоугольника,
то такие прямоугольники равны.

Докажем, что прямоугольники ABDC и EFPH,  изображенные
на рисунке 4 равны между собой.

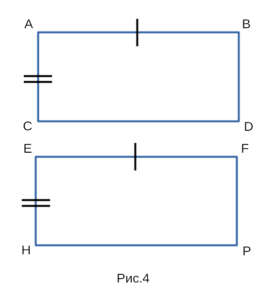
Доказательство четвертого признака равенства
прямоугольников:

1. Рассмотрим прямоугольники ABDC и EFPH, в которых
   AB = EF, AC = EH и AB ∥ EF, AC ∥ EH. Докажем, что
   прямоугольники ABDC и EFPH равны.
2. AB = EF и AB ∥ EF, значит сторону AB можно наложить на
   сторону EF так, что сторона AB совместится со стороной EF.
3. AC = EH и AC ∥ EH, значит сторону AC можно наложить на
   сторону EH так, что сторона AC совместится со стороной EH.
4. Итак, прямоугольники ABDC и EFPH полностью совместятся,
   значит они равны — ч.т.д.

Итог

В этой статье мы доказали равенство прямоугольников по всем четырем признакам.

• Двум неравным сторонам.
• Сумме квадратов двух неравных сторон.
• Диаметру описанной окружности.
• Равным и параллельным противоположным сторонам.