Признаки равенства окружностей

Признаки равенства окружностей — это признаки,
с помощью которых можно доказать, что окружности равны.

В этой статье мы рассмотрим доказательство трех признаков
равенства окружностей. Доказав которые можно научится
уметь решать задачи с доказательством любых признаков
равенства окружностей.

I признак равенства окружностей

По диаметру.

Формулировка:

Если диаметр одной окружности равен диаметру другой окружности, то такие окружности равны.

Докажем, что окружность с диаметром BA и окружность с диаметром DC,  изображенные на рисунке 1 равны между собой.

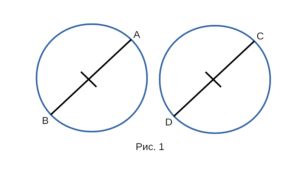
Доказательство:

1. Рассмотрим окружность с диаметром BA и окружность с диаметром DC, в которых BA = DC. Докажем,
   что окружность с диаметром BA и окружность с диаметром DC равны.
2. BA = DC, значит окружность с диаметром BA можно наложить на окружность с диаметром DC так, что они совместятся:
   окружность с диаметром BA совместится с окружностью с диаметром DC.
3. Итак, окружность с диаметром BA и окружность с диаметром DC полностью совместятся, значит они равны — ч.т.д

II признак равенства окружностей

По радиусу.

Формулировка:

Если радиус одной окружности равен радиусу другой окружности, то такие окружности равны.

Докажем, что окружность с радиусом BO и окружность с радиусом DE,  изображенные на рисунке 2 равны между собой.

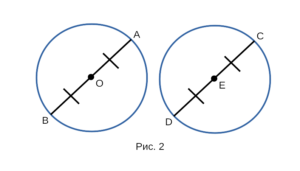
Доказательство:

1. Рассмотрим окружность с радиусом BO и окружность с радиусом DE, в которых BO = DE. Докажем,
   что окружность с радиусом BO и окружность с радиусом DE равны.
2. BO = DE, значит окружность с радиусом BO можно наложить на окружность с радиусом DE так, что они совместятся:
   окружность с радиусом BO совместится с окружностью с радиусом DE.
3. Итак,  окружность с радиусом BO и окружность с радиусом DE полностью совместятся, значит они равны — ч.т.д.

III признак равенства окружностей.

По лучу и углу.

Формулировка:

Если луч делит угол между центрами двух окружностей на два равных угла, то такие окружности равны.

Докажем, что две окружности, изображенные на рисунке 3 равны между собой.

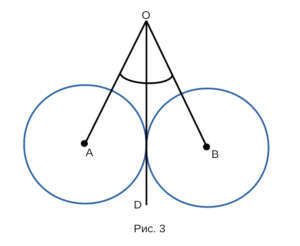
Доказательство:

1. Рассмотрим луч OD, окружность с центром в точке A и окружность с центром в точке В, отрезки OA и OB, в которых ∠AOD = ∠BOD. Докажем,что окружность с центром в точке A и окружность с центром в точке B равны.
   
2. ∠AOD = ∠BOD, значит отрезки OA и OB можно наложить друг на другу так, что они совместятся:
   отрезок OA совместится с отрезком OB.
   
3. Итак, окружность с центром в точке A и окружность с центром в точке B полностью совместятся, значит они равны — ч.т.д.

Итог

В этой статье мы доказали равенство окружностей по всем трем признакам.

• Диаметру.
• Радиусу.
• Лучу и углу.