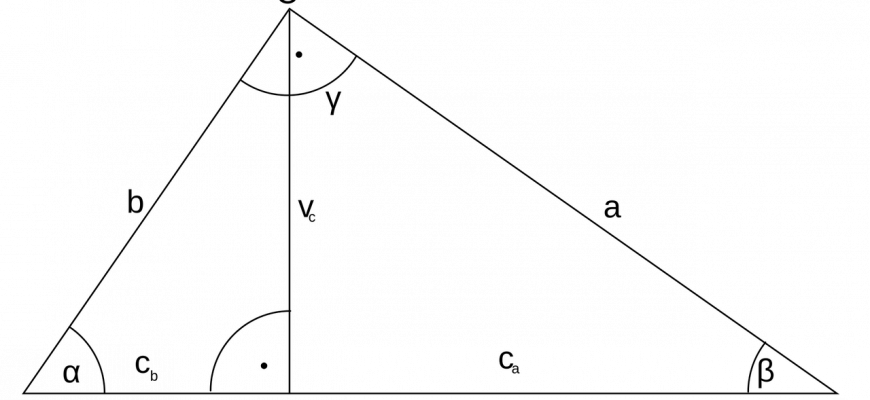
Площадь треугольника через стороны — это
площадь треугольника, которая выражена через
три стороны треугольника и полупериметр.Полупериметр — это половина суммы
длин всех сторон треугольника.
Площадь любого треугольника можно рассчитать по
разным формулам. Одна из популярных формул:
\[ S = \frac{1}{2}ah \]
С помощью этой формулы можно найти площадь
треугольника зная длину основания и высоту.
Но, иногда требуется найти площадь треугольника,
зная только стороны треугольника. Так, как у
каждого треугольника три стороны, то соответственно
три длины. Но, как же найти площадь?
Площадь треугольника через стороны легко рассчитать
зная Формулу Герона.Герон — греческий математик, в
честь которого и была названа эта формула. В чем суть
формулы Герона? Как найти площадь треугольника через длины сторон?
Площадь произвольного треугольника равна квадратному
корню из произведения полупериметра на разницу
между полупериметром и стороной a, полупериметром
и стороной b, полупериметром и стороной c.
Можно сделать вывод, что, чтобы рассчитать площадь треугольника
по Формуле Герона, нужно знать все стороны данного треугольника.
Формула Герона:
\[ S = \sqrt{p(p-a)(p-b)(p-c)} \]
a, b, c — длины сторон треугольника;
p — полупериметр;
S — площадь;
Формула полупериметра:
\[ p = \frac{1}{2}(a+b+c) \]
Обобщение площади треугольника через стороны:
\[ S = \frac{1}{4}\sqrt{(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)} \]
\[ S = \frac{1}{4}\sqrt{(a+b-c)\cdot(a-b+c)\cdot(-a+b+c)\cdot(a+b+c)} \]
\[ S = \frac{1}{4}\sqrt{4a^2+b^2-(a^2+b^2-c^2)^2} \]
Подставив в вышеперечисленные формулы длины всех сторон,
можно найти площадь любого треугольника. С помощью формулы
площади треугольника через три стороны, можно также
найти не только площадь, но и периметр.