Параллелограмм — это выпуклый четырехугольник, у которого
две любые стороны равны и параллельны.
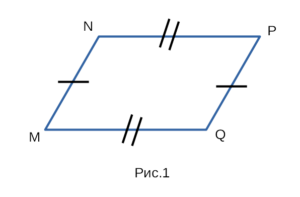
На рисунке 1 изображен выпуклый четырехугольник MNPQ, со сторонами MN, PQ, MQ, NP. Чтобы доказать, что это параллелограмм, посмотрим
какие у него стороны. Итак, по рисунку 1 видно, что у этого выпуклого четырехугольника в первую очередь противоположные стороны равны: MN = PQ и NP = MQ.
Но нам этого еще недостаточно,так как равные противоположные стороны могут быть и у прямоугольника. Для того, чтобы можно было окончательно сказать,
что этот выпуклый четырехугольник — параллелограмм, надо во вторую очередь посмотреть параллельны, ли эти стороны. Сторона MN параллельна стороне PQ,
а сторона NP параллельна стороне MQ. Следовательно, у этого выпуклого четырехугольника две стороны равны и параллельны,а это значит, что это параллелограмм.
Докажем признак, который мы использовали для доказательства — о том, что если в четырехугольнике
две любые стороны равны и параллельны, то это параллелограмм.
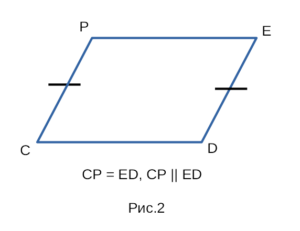
На рисунке 2 изобразим выпуклый четырехугольник CPED. По условию CP = ED, CP || ED. Докажем, что CPED — параллелограмм.
- Проведем диагональ CE, которая разделит выпуклый четырехугольник на два треугольника.
- Рассмотрим два треугольника: CPE и EDC.
- По условию CP = ED.
Сторона CE — общая.
∠ECP=∠CED, так как накрест лежащие углы при СP || ED и секущей CE.Следовательно, по двум сторонам и углу между ними — треугольник CPE равен треугольнику EDC. - Из этого всего следует, что соответствующие углы ∠ECD=∠CPE.
А так как эти углы — накрест лежащие при прямых PE, CD и секущей CE, то прямые PE и CD параллельны.5) PE || CD, CP || ED и PE = CD, CP = ED, следовательно CPED — параллелограмм, ч.т.д.
Признак доказан.
Кроме признака параллелограмма, который мы сейчас доказали, существует еще несколько признаков,
которые мы рассмотрим и докажем в следующих статьях.









