Аксиома стереометрии — это основополагающее
утверждение в стереометрии, не требующее доказательств.Стереометрия — раздел геометрии, изучающий
свойства и признаки фигур в пространстве.
В стереометрии существует три основные аксиомы,
из которых следует остальные не менее важные утверждения.
Свойства точек, прямых а также плоскостей выражены в аксиомах.
Первая аксиома стереометрии
Через любые три точки, не лежащие на одной
прямой проходит плоскость причем только одна.
Плоскость — неограниченная,
ровная поверхность.
Плоскость обозначают тремя буквами
греческого алфавита: α (альфа), β (бета), γ (гамма).
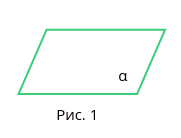
На рисунке 1 изображена плоскость альфа.
Вторая аксиома стереометрии
Если две точки прямой лежат в плоскости,
то и все точки данной прямой лежат в этой плоскости.

Смотрим на рисунок 2 — точка A и точка B прямой a лежат в плоскости β, значит
все точки данной прямой лежат в плоскости β.
Третья аксиома стереометрии
Если две плоскости имеют общую точку, то они
имеют общую прямую, по которой они пересекаются.
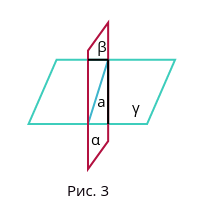
Плоскость γ пересекается с плоскостью α (рисунок 3).