Для начала, чтобы узнать и найти площадь
параллелограмма. Дадим определения
некоторым важным понятиям, связанными так
или иначе с параллелограммом. Это понятие
высоты в параллелограмме и его основания.
Основание параллелограмма — это прямая, на которую
можно опустить перпендикуляр из любой точки
с противоположной стороны параллелограмма.Высота в параллелограмме — это отрезок, являющийся
перпендикуляром, который связывает два основания.
Грубо говоря, если с какой-то из сторон параллелограмма
можно опустить перпендикуляр на противоположную сторону, то
сторона на которую упадет перпендикуляр будет являться
основанием, а сам перпендикуляр — высотой.
Чтобы выразить площадь параллелограмма, нужно
внимательно рассмотреть его. Рассматривая
произвольный параллелограмм, можно заметить,
что он состоит из двух прямоугольных треугольников
и одного прямоугольника. Так, что можно смело заявить:
площадь параллелограмма — это площадь
прямоугольника + площадь двух треугольников.
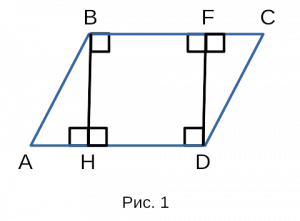
На рисунке 1 изображен параллелограмм ABCD. Площадь S
параллелограмма ABCD, с высотами BH и DF,
равна BF*BH + ½BH*AH + ½FC*FD. Но это очень громоздкая
формула. Математики сократили её и получили современную
формулу площади параллелограмма через высоту и основание.
Площадь S параллелограмма ABCD, с основанием AD
и высотой BH равна AD*BH.
\( S = AD*BH, S = ah \)
Площадь параллелограмма — это площадь фигур,
на которые можно разбить параллелограмм.Площадь параллелограмма численно равна
произведению его основания на высоту.
Теперь, если вы поняли как методом рассмотрения геометрической фигуры,
мы получили площадь параллелограмма, вы сможете найти площадь
большинства других геометрических фигур!









